Trong thành phố Q, để thuận tiện trong việc di chuyển, có n nhà xe đã được xây và đánh số từ 1 tới n. Có m tuyến đường được thiết kế để vận chuyển hành khách giữa các nhà xe A_i và B_i theo 2 chiều, từ nhà xe A_i tới B_i và ngược lại. Mỗi ngày sẽ có 2 chuyến xe để vận chuyển hành khách, 1 chuyến buổi sáng và 1 chuyến buổi chiều của mỗi nhà xe, mỗi chuyến có thể vận chuyển T_i hành khách ứng với mỗi tuyến đường.

Giả sử coi thời gian di chuyển giữa các nhà xe chỉ tốn 1 buổi sáng hoặc 1 buổi chiều, hãy tính lượng hành khách tối đa có thể vận chuyển giữa nhà xe X_i và Y_i trong 1 ngày. Có 2 cách đi, cách đầu tiên là đi trực tiếp từ nhà xe X_i tới nhà xe Y_i nếu tồn tại tuyến đường đi thẳng, cách thứ 2 là bắt 1 chuyến xe từ nhà xe X_i tới 1 nhà xe trung gian P_i vào buổi sáng và từ nhà xe P_i tới nhà xe Y_i vào buổi chiều nếu tồn tại tuyến đường kết nối 2 nhà xe với nhà xe trung gian.

Yêu cầu: Để đáp ứng nhu cầu vận chuyển, bạn hãy tính toán cho q truy vấn. Mỗi truy vấn bạn hãy xác định lượng hành khách tối đa có thể vận chuyển giữa 2 nhà xe X_i và Y_i.

Dữ liệu vào:

• Dòng đầu tiên chứa ba số nguyên n, m và q.
• m dòng tiếp theo, mỗi dòng gồm 3 số tự nhiên u, v và c tương ứng với tuyến đường giữa 2 nhà xe u-v và mỗi chuyến xe có thể chở tối đa c hành khách.
• q dòng tiếp theo, mỗi dòng gồm 2 số tự nhiên x và y ứng với truy vấn tìm lượng hành khách tối đa có thể vận chuyển giữa 2 nhà xe trong 1 ngày.

Dữ liệu ra:

• Gồm q dòng, mỗi dòng là kết quả ứng với mỗi truy vấn.

Input:

7 7 5
1 2 20
1 3 30
2 3 15
2 4 30
3 4 20
5 6 70
4 7 90
1 2
1 4
2 3
1 6
1 7

Output:

55
40
70
0
0

Giải thích:

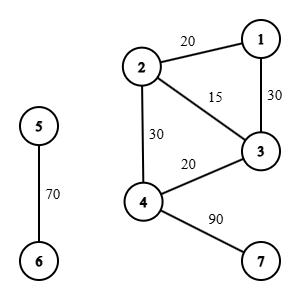
• Hình trên miêu tả đồ thị kết nối các nhà xe, được đánh số lần lượt từ 1 tới 7

• Truy vấn 1: Với cách đi trực tiếp từ nhà xe 1 tới nhà xe 2, ta có thể vận chuyển 40 hành khách (20 cho chuyến buổi sáng và 20 cho chuyến buổi chiều). Với cách đi gián tiếp qua nhà xe 3, ta vận chuyển 30 hành khách từ nhà xe 1 tới nhà xe 3 trong chuyến buổi sáng, chuyến buổi chiều ta chỉ có thể vận chuyển tối đa 15 hành khách từ nhà xe 3 tới nhà xe 2. Tổng cộng, tối đa 20*2 + 15 = 55 hành khách được vận chuyển.

• Truy vấn 2: Ta chỉ có thể đi từ nhà xe 1 tới nhà xe 4 thông qua cách đi gián tiếp (qua nhà ga 2 hoặc 3). Với cách đi qua nhà xe 2, ta có thể vận chuyển 20 hành khách, tương tự với nhà xe 3 là 20. Tổng cộng, tối đa 20+20=40 hành khách được vận chuyển.

• Truy vấn 3: Có 3 cách đi (trực tiếp và gián tiếp thông qua nhà xe 1 và 4). Cách trực tiếp vận chuyển được 30 hành khách, với 2 cách đi gián tiếp thì đều vận chuyển được, mỗi cách 20. Tổng cộng có 20 + 20 + 30 = 70 hành khách.

• Truy vấn 4: Không tồn tại cách đi trực tiếp hay gián tiếp để đi từ nhà xe 1 tới nhà xe 6. Do đó có 0 hành khách có thể vận chuyển.

• Truy vấn 5: Không tồn tại cách di chuyển gián tiếp để đi từ nhà xe 1 tới nhà xe 7 trong 1 ngày! Do đó có 0 hành khách có thể vận chuyển.

Giới hạn:

• ~1 \le n, m, q \le 2*10^{5}~.
• ~1 \le T_i \le 10^{9}~.
• ~1 \le A_i, B_i \le n~, ~A_i \neq B_i~.
• ~1 \le X_i, Y_i \le n~, ~X_i \neq Y_i~.
• Các cặp (~A_i, B_i~) đôi một khác nhau.