Cô Q cho các bạn N điểm trong hệ tọa độ Oxy, mỗi điểm có tọa độ (x, y). Hãy đếm xem có bao nhiêu hình vuông có thể tạo thành từ các bộ 4 điểm trong N điểm ấy.

Dữ liệu vào:

• Dòng đầu tiên chứa số nguyên N.
• N dòng tiếp theo, mỗi dòng chứa 2 số nguyên x, y là tọa độ của mỗi điểm.

Dữ liệu ra:

• Gồm 1 dòng duy nhất là số lượng các bộ 4 điểm tạo thành hình vuông.

Input:

11
0 0
2 2
2 -2
4 0
4 2
4 -2
5 2
5 -2
6 0
6 2
6 -2

Output:

4

Giải thích:

-

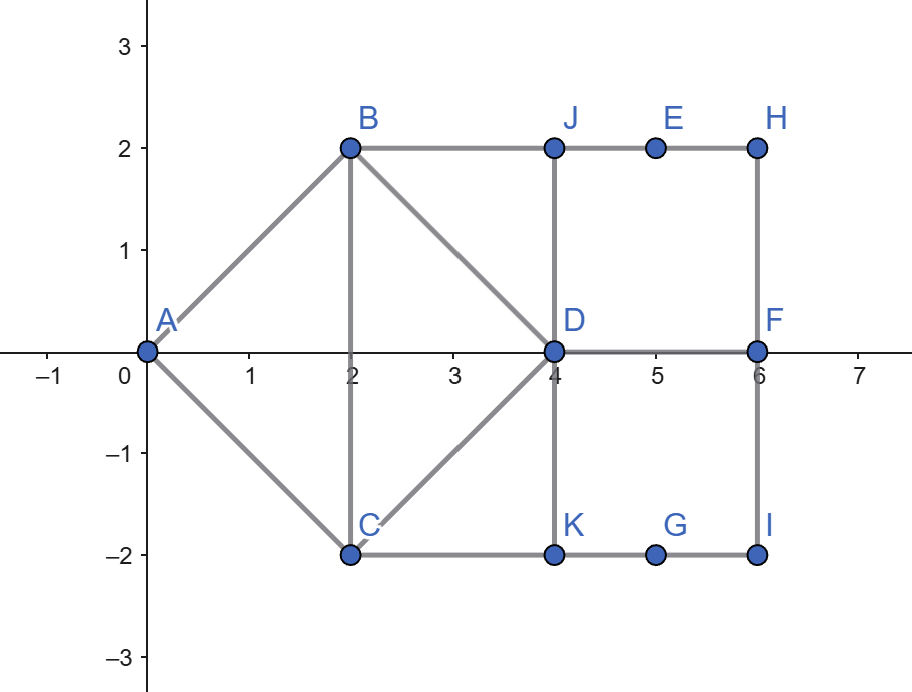
• Hình trên miêu tả vị trí 11 điểm, tương ứng là A(0, 0), B(2, 2), C(2, -2), D(4, 0), E(5, 2), F(6, 0), G(5, -2), H(6, 2), I(6, -2), J(4, 2), K(4, -2).
• Có 4 hình vuông lần lượt là: ABDC, BHIC, JHFD, DFIK.
• Lưu ý: Đa giác EFGD là hình thoi (không phải là hình vuông, dù có 4 cạnh bằng nhau).

Giới hạn:

• ~1 \le n \le 50~.
• ~-1000 \le x_i, y_i \le 1000~.
• Các cặp (~x_i, y_i~) đôi một khác nhau.

Cô Q là 1 người yêu thích về tập hợp nên cô giao cho các bạn sinh viên 1 bài tập như sau.

Cho dãy n phần tử a₁, a₂, ... a_n và số nguyên k. Hãy đếm xem có bao nhiêu tập hợp con khác rỗng sao cho tổng các phần tử của tập hợp con chia hết cho k.

Dữ liệu vào:

• Dòng đầu tiên chứa hai số nguyên n và k.
• Dòng tiếp theo chứa n số tự nhiên a₁, a₂, ... a_n.

Dữ liệu ra:

• 1 dòng chứa số lượng tập hợp con khác rỗng sao cho tổng các phần tử của chúng chia hết cho k.

Input:

3 2
1 2 3

Output:

3

Giải thích:

• Có 3 tập hợp con {2}, {1, 3}, {1, 2, 3} thỏa mãn.

Giới hạn:

• ~1 \le n \le 20~, ~2 \le k \le 100~.
• ~1 \le a_i \le 10^{6}~.

Trong phòng thí nghiệm Khoa học Vật Liệu ở Đại học Phenikaa, cô Q đang nghiên cứu quá trình kết tinh gốm. Khi gốm nguội dần, các tinh thể nhỏ dần dần mọc lên và sao chép hình dạng của chính mình ở nhiều cấp độ — hiện tượng này gọi là tự đồng dạng (self-similarity), hay còn gọi là mô hình fractal trong toán học. Để mô phỏng hiện tượng này, cô Q muốn tạo một mẫu tinh thể fractal hình chữ thập, trong đó mỗi cấp tinh thể mới được tạo ra bằng cách ghép 5 bản sao của tinh thể cấp trước. Bạn hãy giúp cô Q làm điều ấy nhé.

Yêu cầu: Cho một số nguyên N – thể hiện cấp độ phát triển của tinh thể. Hãy xây dựng mẫu tinh thể fractal theo quy tắc sau:

• Ở mỗi cấp N, ma trận biểu diễn sẽ có kích thước là ~3^{N-1}~ x ~3^{N-1}~.
• Ở cấp 1, tinh thể chỉ là một ô duy nhất, ký hiệu X.
• Ở cấp 2, là sự mở rộng của cấp 1, ta thêm 4 tinh thể cấp 1 theo bốn hướng trên – dưới – trái – phải so với cấp 1. Các ô trống còn lại được ký hiệu bằng dấu .
• Ở cấp 3, là sự mở rộng của cấp 2, ta thêm 4 mẫu tinh thể cấp 2 theo bốn hướng trên – dưới – trái – phải so với cấp 2. Các ô trống còn lại được ký hiệu bằng dấu .
• Cứ tiếp tục lặp lại như vậy cho đến cấp N. Là sự mở rộng của cấp N - 1, ta thêm 4 mẫu tinh thể cấp N - 1 theo bốn hướng trên – dưới – trái – phải so với cấp N - 1. Các ô trống còn lại được ký hiệu bằng dấu .

Dữ liệu vào:

• Gồm 1 dòng chứa 1 số tự nhiên N.

Dữ liệu ra:

• Ma trận có kích thước ~3^{N-1}~ x ~3^{N-1}~ biểu diễn hình học fractal của tinh thể.

Input 1:

1

Output 1:

X

Input 2:

2

Output 2:

.X.
XXX
.X.

Input 3:

3

Output 3:

....X....
...XXX...
....X....
.X..X..X.
XXXXXXXXX
.X..X..X.
....X....
...XXX...
....X....

Giới hạn:

• ~1 \le N \le 7~.

Cô Q tổ chức 1 trò chơi xổ số may mắn cho các bạn sinh viên tham gia. Có N tấm vé được đánh số từ 1 tới N. Mỗi tấm vé có xác suất bằng nhau được chọn trúng thưởng. Tuy nhiên phần thưởng có quy luật đặc biệt như sau:

• Nếu vé chia hết cho K, sẽ được A điểm thưởng.
• Nếu vé chia K dư R, sẽ được B điểm thưởng.
• Còn lại thì được 0 điểm thưởng.

Yêu cầu: Cô Q yêu cầu hãy tính giá trị thưởng kỳ vọng đạt được nếu chỉ mua 1 vé ngẫu nhiên trong N vé.

Dữ liệu vào:

• 1 dòng duy nhất chứa các số tự nhiên N, K, R, A và B.

Dữ liệu ra:

• Giá trị thưởng kỳ vọng khi mua 1 vé ngẫu nhiên trong N vé, làm tròn kết quả tới 5 chữ số sau phần thập phân.

Input:

10 4 2 3 7

Output:

2.70000

Giải thích:

• Ta có N = 10, K = 4, R = 2, A = 3, B = 7.
• Với N % K = 0, ta có N = 4 và N = 8 thỏa
• Với N % K = 2, ta có N = 2, N = 6, N = 10 thỏa
• Do đó giá trị kỳ vọng là (2 * 3 + 3 * 7) / 10 = 2.70000

Giới hạn:

• ~10 \le N \le 10^{6}~, ~3 \le K \le {N-1}~, ~1 \le R \le K-1~.
• ~1 \le A, B \le 10^6~.

Cô Q đang hợp tác với Viện Vật liệu tại Bắc Ninh để nghiên cứu vật liệu gốm xốp ứng dụng trong lọc nước. Lớp gốm này có cấu trúc đa por (đa lỗ) với độ không đồng nhất cao. Các thử nghiệm thực tế cho thấy khi áp dụng quy trình etching hóa học (khắc hóa học), các vùng có độ bền thấp (ngưỡng ăn mòn nhỏ) sẽ bị ăn mòn trước, hình thành lỗ rỗng lan dần. Khi ngưỡng ăn mòn T đủ lớn, sẽ xuất hiện một đường thông từ mặt trên đến mặt dưới, cho phép dòng nước xuyên qua

Trên cơ sở này, ta giả lập màng gốm xốp dưới dạng lưới vuông có kích thước 𝑁×𝑁. Mỗi ô (i,j) có độ bền vật liệu (ngưỡng ăn mòn) a_(i,j). Khi etch ở mức T, ô bị ăn mòn (rỗng) nếu a_(i,j) ~\le T~, ngược lại vẫn đặc. Khi T tăng dần, càng nhiều ô bị ăn mòn, và có thể sẽ xuất hiện một đường thông từ hàng trên cùng xuống hàng dưới cùng, cho phép nước thấm xuyên qua màng. Cô Q quan tâm: ngưỡng tối thiểu T để dòng nước thấm từ hàng trên cùng xuống hàng dưới cùng và có thể đi qua màng.

Yêu cầu: Tìm giá trị nhỏ nhất T sao cho khi đánh dấu tất cả các ô có a_(i,j) ~\le T~ là rỗng, tồn tại một đường đi liên thông qua các ô rỗng từ ô bất kỳ thuộc hàng đầu tiên đến bất kỳ ô thuộc hàng N.

Định nghĩa về liên thông: Hai ô được gọi là liên thông nếu:

• Chúng đều là ô rỗng, và
• Chúng kề cạnh nhau theo 1 trong 4 hướng cơ bản: Trên, dưới, trái, phải.

Dữ liệu vào:

• Dòng đầu tiên chứa số nguyên N.
• N dòng tiếp theo, mỗi dòng gồm N số tự nhiên biểu thị ngưỡng ăn mòn.

Dữ liệu ra:

• Kết quả T là giá trị ngưỡng nhỏ nhất.

Input:

3
5 4 7
6 2 8
9 1 3

Output:

4

Giải thích:

• Với T = 4, thì các ô có giá trị 4, 2, 1 sẽ tạo thành 1 thành phần liên thông từ hàng 1 tới hàng N.

Giới hạn:

• ~1 \le N \le 10^{3}~.
• ~0 \le a_{i,j} \le 10^{9}~.

Cô Q rất thích vẻ đẹp của sự đối xứng nên cô cho các bạn sinh viên 1 bài tập nhẹ nhàng như sau. Cho 1 xâu s bao gồm chuỗi các ký tự Latin in thường có độ dài n. Hãy kiểm tra xem xâu ấy có phải là xâu đối xứng cấp 2 không.

Một xâu s được gọi là đối xứng cấp 2 nếu chúng thỏa mãn các điều kiện sau:

• Xâu s là xâu đối xứng.
• Xâu s được tạo thành bằng cách ghép 2 xâu đối xứng không rỗng lại.

Dữ liệu vào:

• Dòng đầu tiên chứa số nguyên n.
• Dòng thứ 2 chứa xâu s độ dài n.

Dữ liệu ra:

• In ra YES nếu là xâu đối xứng cấp 2, NO nếu không phải.

Input:

6
abaaba

Output:

YES

Giới hạn:

• ~1 \le n \le 1000~.

Trong thành phố Q, để thuận tiện trong việc di chuyển, có n nhà xe đã được xây và đánh số từ 1 tới n. Có m tuyến đường được thiết kế để vận chuyển hành khách giữa các nhà xe A_i và B_i theo 2 chiều, từ nhà xe A_i tới B_i và ngược lại. Mỗi ngày sẽ có 2 chuyến xe để vận chuyển hành khách, 1 chuyến buổi sáng và 1 chuyến buổi chiều của mỗi nhà xe, mỗi chuyến có thể vận chuyển T_i hành khách ứng với mỗi tuyến đường.

Giả sử coi thời gian di chuyển giữa các nhà xe chỉ tốn 1 buổi sáng hoặc 1 buổi chiều, hãy tính lượng hành khách tối đa có thể vận chuyển giữa nhà xe X_i và Y_i trong 1 ngày. Có 2 cách đi, cách đầu tiên là đi trực tiếp từ nhà xe X_i tới nhà xe Y_i nếu tồn tại tuyến đường đi thẳng, cách thứ 2 là bắt 1 chuyến xe từ nhà xe X_i tới 1 nhà xe trung gian P_i vào buổi sáng và từ nhà xe P_i tới nhà xe Y_i vào buổi chiều nếu tồn tại tuyến đường kết nối 2 nhà xe với nhà xe trung gian.

Yêu cầu: Để đáp ứng nhu cầu vận chuyển, bạn hãy tính toán cho q truy vấn. Mỗi truy vấn bạn hãy xác định lượng hành khách tối đa có thể vận chuyển giữa 2 nhà xe X_i và Y_i.

Dữ liệu vào:

• Dòng đầu tiên chứa ba số nguyên n, m và q.
• m dòng tiếp theo, mỗi dòng gồm 3 số tự nhiên u, v và c tương ứng với tuyến đường giữa 2 nhà xe u-v và mỗi chuyến xe có thể chở tối đa c hành khách.
• q dòng tiếp theo, mỗi dòng gồm 2 số tự nhiên x và y ứng với truy vấn tìm lượng hành khách tối đa có thể vận chuyển giữa 2 nhà xe trong 1 ngày.

Dữ liệu ra:

• Gồm q dòng, mỗi dòng là kết quả ứng với mỗi truy vấn.

Input:

7 7 5
1 2 20
1 3 30
2 3 15
2 4 30
3 4 20
5 6 70
4 7 90
1 2
1 4
2 3
1 6
1 7

Output:

55
40
70
0
0

Giải thích:

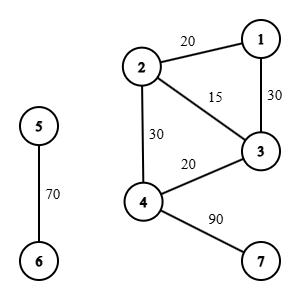
• Hình trên miêu tả đồ thị kết nối các nhà xe, được đánh số lần lượt từ 1 tới 7

• Truy vấn 1: Với cách đi trực tiếp từ nhà xe 1 tới nhà xe 2, ta có thể vận chuyển 40 hành khách (20 cho chuyến buổi sáng và 20 cho chuyến buổi chiều). Với cách đi gián tiếp qua nhà xe 3, ta vận chuyển 30 hành khách từ nhà xe 1 tới nhà xe 3 trong chuyến buổi sáng, chuyến buổi chiều ta chỉ có thể vận chuyển tối đa 15 hành khách từ nhà xe 3 tới nhà xe 2. Tổng cộng, tối đa 20*2 + 15 = 55 hành khách được vận chuyển.

• Truy vấn 2: Ta chỉ có thể đi từ nhà xe 1 tới nhà xe 4 thông qua cách đi gián tiếp (qua nhà ga 2 hoặc 3). Với cách đi qua nhà xe 2, ta có thể vận chuyển 20 hành khách, tương tự với nhà xe 3 là 20. Tổng cộng, tối đa 20+20=40 hành khách được vận chuyển.

• Truy vấn 3: Có 3 cách đi (trực tiếp và gián tiếp thông qua nhà xe 1 và 4). Cách trực tiếp vận chuyển được 30 hành khách, với 2 cách đi gián tiếp thì đều vận chuyển được, mỗi cách 20. Tổng cộng có 20 + 20 + 30 = 70 hành khách.

• Truy vấn 4: Không tồn tại cách đi trực tiếp hay gián tiếp để đi từ nhà xe 1 tới nhà xe 6. Do đó có 0 hành khách có thể vận chuyển.

• Truy vấn 5: Không tồn tại cách di chuyển gián tiếp để đi từ nhà xe 1 tới nhà xe 7 trong 1 ngày! Do đó có 0 hành khách có thể vận chuyển.

Giới hạn:

• ~1 \le n, m, q \le 2*10^{5}~.
• ~1 \le T_i \le 10^{9}~.
• ~1 \le A_i, B_i \le n~, ~A_i \neq B_i~.
• ~1 \le X_i, Y_i \le n~, ~X_i \neq Y_i~.
• Các cặp (~A_i, B_i~) đôi một khác nhau.

Cô Q hôm nay cho các em sinh viên thực hành về mạng tích chập CNN (Convolutional Neural Network) để giúp các em hiểu rõ cách hoạt động của CNN trong xử lý ảnh.

Cô Q cho các em 1 ảnh có kích thước N X N và kích thước của bộ lọc (Kernel) là K X K. Sau khi bộ lọc quét qua ảnh, ảnh sẽ có kích thước (N - K + 1) x (N - K + 1). Cô Q yêu cầu các em hãy tính ảnh đầu ra sau khi kernel quét qua ảnh. Trong bài toán này, công thức được định nghĩa với pixel có tọa độ (i, j) của ảnh đầu ra như sau:

\[ O_{i,j} = \sum_{u=0}^{K-1} \sum_{v=0}^{K-1} I_{i+u,\,j+v}\,K_{u,v} \]

Yêu cầu: Hãy thực hiện yêu cầu của cô Q.

Dữ liệu vào:

• Dòng đầu tiên chứa 2 số nguyên N và K.
• N dòng tiếp theo, mỗi dòng gồm N số tự nhiên tương ứng với giá trị của mỗi pixel trên ảnh.
• K dòng tiếp theo, mỗi dòng gồm K số tự nhiên tương ứng với giá trị của từng phần tử trong kernel.

Dữ liệu ra:

• Gồm N-K+1 dòng, mỗi dòng gồm N-K+1 số biểu thị kết quả sau khi chạy lớp kernel.

Input:

4 2
1 2 3 4
5 6 7 8
9 8 7 6
5 4 3 2
1 0
0 -1

Output:

-5 -5 -5
-3 -1  1
 5  5  5

Giải thích:

• O_0,1 = 1x1 + 2x0 + 5x0 + 6x(-1) = 1 - 6 = -5
• O_0,1 = 2×1 + 3×0 + 6×0 + 7×(-1) = 2 - 7 = -5
• O_0,2 = 3×1 + 4×0 + 7×0 + 8×(-1) = 3 - 8 = -5
• O_1,0 = 5×1 + 6×0 + 9×0 + 8×(-1) = 5 - 8 = -3
• O_1,1 = 6×1 + 7×0 + 8×0 + 7×(-1) = 6 - 7 = -1
• O_1,2 = 7×1 + 8×0 + 7×0 + 6×(-1) = 7 - 6 = 1
• O_2,0 = 9×1 + 8×0 + 5×0 + 4×(-1) = 9 - 4 = 5
• O_2,1 = 8×1 + 7×0 + 4×0 + 3×(-1) = 8 - 3 = 5
• O_2,2 = 7×1 + 6×0 + 3×0 + 2×(-1) = 7 - 2 = 5

Giới hạn:

• ~1 \le N, K \le 50, K \le N~.
• Các pixel trong ảnh có giá trị nằm trong khoảng ~[0, 255]~.
• Các phần tử trong kernel có giá trị nằm trong khoảng ~[-2, 2]~.

Trong 1 kỳ thi về robot, chị Q được yêu cầu lập trình để tính toán số thao tác ít nhất để robot từ vị trí (a, b) tới lấy đồ tại vị trí (c, d). Robot di chuyển trên hệ tọa độ Oxy, robot có thể thực hiện 1 trong 4 thao tác di chuyển sau:

• U di chuyển từ tọa độ (x, y) tới (x-1, y),
• D di chuyển từ tọa độ (x, y) tới (x+1, y),
• L di chuyển từ tọa độ (x, y) tới (x, y-1),
• R di chuyển từ tọa độ (x, y) tới (x, y+1).

Yêu cầu:
Hãy in ra số thao tác ít nhất để robot từ vị trí (a, b) tới lấy đồ tại vị trí (c, d).

Dữ liệu vào:

• 1 dòng tiếp theo, mỗi dòng gồm 4 số nguyên a b c d.

Dữ liệu ra:

• Gồm 1 dòng, in ra số thao tác ít nhất cần thực hiện.

Input:

1 1 3 3

Output:

4

Giải thích:

1 cách đi ngắn nhất là thực hiện chuỗi thao tác DDRR tương ứng với ~(1, 1) \to (2, 1) \to (3, 1) \to (3, 2) \to (3, 3)~.

Giới hạn:

• ~-10^{6} \le |a|, |b|, |c|, |d| \le 10^{6}~.

Cô Q rất yêu thích toán học nên đã đố các bạn 1 bài toán như sau.

Cho hai số nguyên k và n. Ta định nghĩa công thức mở rộng của dãy Fibonacci như sau (gọi là k-bonacci):

• F^(k)₁ = a₁, F^(k)₂ = a₂, ..., F^(k)_k = a_k.
  Với a₁, a₂, ..., a_k là các số tự nhiên.

• Với n > k:
  F^(k)_n = F^(k)_n-1 + F^(k)_n-2 + … + F^(k)_n-k.

Ta định nghĩa tổng của n số k-bonacci đầu tiên như sau:

• S^(k)(n) = F^(k)₁ + F^(k)₂ + … + F^(k)_n.

Yêu cầu: Bạn hãy tính S^(k)(n) mod (~10^{9} + 7~).

Dữ liệu vào:

• Dòng đầu tiên chứa hai số nguyên k và n.
• Dòng thứ hai gồm k số tự nhiên a₁, a₂, ..., a_k.

Dữ liệu ra:

• Một số nguyên duy nhất là kết quả của phép tính S^(k)(n) mod (~10^{9} + 7~).

Input:

3 4
1 1 2

Output:

8

Giới hạn:

• ~2 \le k \le 100~, ~1 \le n \le 10^{18}~.
• ~1 \le a_1, a_2, ..., a_k \le 10^9~

Cô Q Cho số nguyên dương ~n~. Hãy kiểm tra xem số nguyên dương ~n~ có phải là số nguyên tố không. Nếu đúng in ra YES, nếu không in ra NO.

Dữ liệu vào:

• Một dòng duy nhất chứa số nguyên ~n~.

Dữ liệu ra:

• Một số nguyên duy nhất là YES nếu số nguyên dương ~n~ là số nguyên tố, ngược lại in ra NO.

Input:

8

Output:

NO

Giới hạn:

• ~1 \le n \le 10^6~.

Cô Q cho 1 xâu s bao gồm chuỗi các ký tự Latin in thường có độ dài n. Bạn được cho q truy vấn, có 2 loại truy vấn, mỗi loại truy vấn có dạng như sau:

• Truy vấn loại 1: pos char. Thay đổi ký tự ở vị trí pos sang ký tự char.
• Truy vấn loại 2: L R. Kiểm tra xem xâu con s[L...R] có phải là xâu đối xứng không.

Dữ liệu vào:

• Dòng đầu tiên chứa 2 số nguyên n và q.
• Dòng thứ 2 chứa xâu s độ dài n.
• q dòng tiếp theo chứa các truy vấn có dạng. 1 pos char tương ứng với truy vấn 1. 2 L R tương ứng với truy vấn 2.

Dữ liệu ra:

• q dòng tiếp theo chứa kết quả tương ứng của truy vấn 2. In ra YES nếu xâu con là xâu đối xứng, NO nếu xâu con không là xâu đối xứng.

Input:

7 5
aybabtu
2 3 5
1 3 x
2 3 5
1 5 x
2 3 5

Output:

YES
NO
YES

Giới hạn:

• ~n \le 2*10^5, q \le 2*10^5~.
• ~1 \le L \le R \le n~.

Trong thành phố Q có n khu dân cư được đánh số từ 1 tới n. Các thành phố được kết nối với nhau thông qua các n - 1 tuyến đường 2 chiều, đảm bảo các khu dân cư đến được với nhau thông qua các con đường.

Lãnh đạo thành phố Q xây bệnh viện ở 1 số khu dân cư để phục vụ nhu cầu khám chữa bệnh cho người dân. Có k bệnh viện được xây ở k khu dân cư, hãy giúp người dân xác định khoảng cách ngắn nhất tới bệnh viện gần nhất.

Định nghĩa khoảng cách ngắn nhất từ khu dân cư tới bệnh viện: Là số tuyến đường ít nhất để đi từ khu dân cư tới bệnh viện.

Yêu cầu: Bạn được cho t truy vấn. Mỗi truy vấn bạn hãy xác định khoảng cách ngắn nhất của 1 khu dân cư tới bệnh viện gần nhất.

Dữ liệu vào:

• Dòng đầu tiên chứa ba số nguyên n, k và t.
• Dòng thứ hai gồm k số tự nhiên đôi một khác nhau a₁, a₂, ..., a_k, tương ứng với k bệnh viện.
• n - 1 dòng tiếp theo, mỗi dòng gồm 2 số tự nhiên u và v là tuyến đường nối giữa 2 thành phố u và v.
• t dòng tiếp theo, mỗi dòng gồm 1 số tự nhiên city ứng với truy vấn tìm khoảng cách tới bệnh viện gần nhất.

Dữ liệu ra:

• Gồm t dòng, mỗi dòng là kết quả ứng với mỗi truy vấn.

Input:

9 3 5
3 4 6
1 2
2 3
2 4
4 5
5 8
6 7
5 7
5 9
1
2
4
5
8

Output:

2
1
0
1
2

Giải thích:

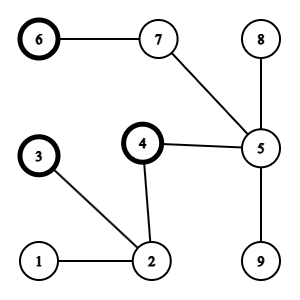
• Hình trên miêu tả đồ thị kết nối các thành phố. Có 3 bệnh viện ở khu dân cư lần lượt là 3, 4, 6.
• Có 5 truy vấn
• Truy vấn 1: Cần tìm khoảng cách bệnh viện ngắn nhất tới khu dân cư 1. Bệnh viện ở khu dân cư 3 hoặc 4 gần nhất với khoảng cách 2.
• Truy vấn 2: Cần tìm khoảng cách bệnh viện ngắn nhất tới khu dân cư 2. Bệnh viện ở khu dân cư 3 hoặc 4 gần nhất với khoảng cách 1.
• Truy vấn 3: Cần tìm khoảng cách bệnh viện ngắn nhất tới khu dân cư 4. Bệnh viện ở khu dân cư 4 nên không cần đi đâu cả! (Khoảng cách 0).
• Truy vấn 4: Cần tìm khoảng cách bệnh viện ngắn nhất tới khu dân cư 5. Bệnh viện ở khu dân cư 4 gần nhất với khoảng cách 1.
• Truy vấn 5: Cần tìm khoảng cách bệnh viện ngắn nhất tới khu dân cư 8. Bệnh viện ở khu dân cư 4 gần nhất với khoảng cách 2.

Giới hạn:

• ~5 \le n \le 10^{6}~, ~1 \le k < n, 1 \le t \le n~.
• ~1 \le a_1, a_2, ..., a_k \le n~

Trong lĩnh vực phát hiện đối tượng (Object Detection), người ta thường sử dụng chỉ số IOU (Intersection over Union) để đánh giá mức độ trùng khớp giữa hộp chứa chuẩn (ground truth bounding box) và hộp chứa dự đoán (predicted bounding box). Chỉ số này được định nghĩa như sau:

$$ IOU = \frac{\text{Diện tích phần giao nhau (Intersection)}}{\text{Diện tích phần hợp nhất (Union)}} $$

Nhiệm vụ

Bạn được cho nhiều testcase, mỗi testcase bao gồm:

• Tọa độ của hai hình chữ nhật (bounding box) trên mặt phẳng tọa độ:
• Hộp chứa chuẩn (Ground Truth): Gồm 4 cặp tọa độ tương ứng với 4 đỉnh của hình chữ nhật $$(x_1, y_1), (x_2, y_2), (x_3, y_3), (x_4, y_4)$$.
• Hộp chứa dự đoán (Predicted Box): Gồm 4 cặp tọa độ tương ứng với 4 đỉnh của hình chữ nhật $$(x'_1, y'_1), (x'_2, y'_2), (x'_3, y'_3), (x'_4, y'_4)$$.

Dữ liệu vào:

• Dòng đầu tiên là số lượng testcase T.
• Với các mỗi testcase, data đầu vào sẽ có dạng.
• $$(x_1, y_1), (x_2, y_2), (x_3, y_3), (x_4, y_4)$$
• $$(x'_1, y'_1), (x'_2, y'_2), (x'_3, y'_3), (x'_4, y'_4)$$
• Các hình chữ nhật đều được đảm bảo là song song với trục hoành hoặc trục tung của hệ tọa độ Oxy.

Dữ liệu ra:

• Gồm ~T~ dòng, mỗi dòng là chỉ số IOU tương ứng. Hãy làm tròn kết quả đến 5 chữ số sau phần thập phân.

Input:

2
0 0 0 2 2 2 2 0
1 1 1 3 3 3 3 1
0 0 0 3 3 3 3 0
3 3 3 6 6 6 6 3

Output:

0.14286
0.00000

Giới hạn:

• ~1 \le T \le 1000~.
• Các tọa độ là các số nguyên nằm trong khoảng ~[0, 10^6]~.